Command manual

Command list

OUTPUT_SENSOR_EXTENDED

Output
Attention: This command is in the beta stage and the format may change over time.
*OUTPUT_SENSOR_EXTENDED
"python_file_name"
coid
sid${}_0$, sid${}_1$, $\Delta t_{out}$, fid${}_1$, ..., fid${}_5$
"name${}_1$"
"name${}_2$"
.
"name${}_n$"

Parameter definition

VariableDescription
python_file_name Name of python file
coid Command ID
sid${}_0$ ID of first sensor in range (see OUTPUT_SENSOR)
sid${}_1$ ID of last sensor in range (see OUTPUT_SENSOR)
$\Delta t_{out}$ Output interval
default: $\Delta t_{out} = \Delta t_{ascii}$
fid${}_1$, ..., fid${}_5$ Optional functions used in sensor calculations
name${}_1$ Name of variable 1
name${}_2$ Name of variable 2
name${}_n$ Name of variable n

Description

This command is used to add complex user defined variables (signals) to existing sensors (see OUTPUT_SENSOR). Variables are automatically defined by declaring their names ("name${}_1$" to "name${}_n$").

All calculations are done in a python script "python_file_name.py". The script must contain the two functions "init" and "update". "init" is called at time 0 and it is used to set intitial variable values. "update" is called every time step and it is used to compute/update the sensor variables.

The computed values are written to the time history file "python_file_name_X.out", where X=coid.

Arguments to the python "update" function are the sensor variables "name${}_1$" to "name${}_n$", followed by current time, current time step size, effective plastic strain, effective creep strain, damage level, temperature, stress components (6), strain components (6), velocity components (3), current coordinate (3) and finally (if defined) the optional function values fid${}_1$ to fid${}_5$.

Example

Compare two different damage models

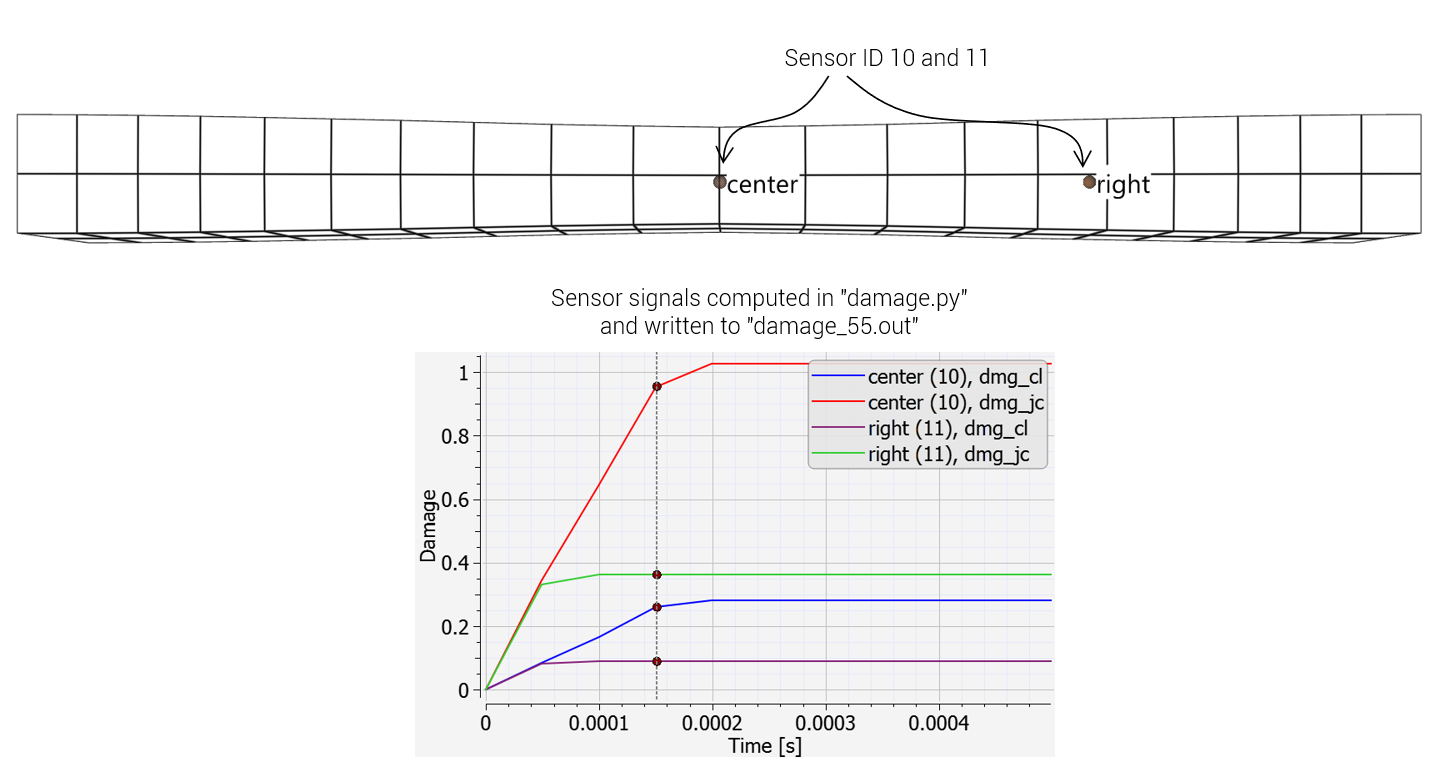
A model using OUTPUT_SENSOR_EXTENDED to test and compare two different damage models (Cockcroft-Latham and Johnson-Cook). The damage evolution is evaluated at the sensors with ID's 10 and 11. The results are output to the file "damage_55.out".


Command file:

*UNIT_SYSTEM
SI
*SCRIPT_PYTHON
damage.py
*TIME
5.0e-4
#
# --- SENSORS ---
#
*OUTPUT_SENSOR
"center"
10, 1, 0, 0, 0
"right"
11, 1, 0.05, 0, 0
*OUTPUT_SENSOR_EXTENDED
"damage"
55
10, 11, 5.0e-5
"dmg_cl"
"dmg_jc"
"epsp"
#
# --- MESH ---
#
*COMPONENT_BOX
"sample"
1, 1, 20, 2, 2
-0.1, -0.01, -0.01, 0.1, 0.01, 0.01
#
# --- MATERIAL ---
#
*MAT_METAL
1, 7800.0, 210.0e9, 0.3, 0, 1
1
*FUNCTION
1
5.0e8 + 5.0e8*epsp^0.3
*PROP_THERMAL
1, 0.0, 450.0
#
# --- PART ---
#
*PART
"sample"
1, 1
#
# --- INITIAL VELOCITY ---
#
*INITIAL_VELOCITY
P, 1, fcn(123)
*FUNCTION
123
3000*x
*END

Python script damage.py:

#

# COMPARISON OF DAMAGE MODELS

#   dmg_cl - Cockcroft-Latham

#   dmg_jc - Johnson-Cook

#

import math

 

# damage parameters

Wc    = 1.0e9

d1    = 0.1

d2    = 0.3

d3    = 0.5

d4    = 0.01

d5    = 0.7

eps_0 = 1.0

T_0   = 0.0

T_m   = 1500.0



#

# INITIALIZE DAMAGE

def init():

    return [0, 0, 0] 

#

# UPDATE DAMAGE

def update(dmg_cl, dmg_jc, epsp_old,

           t, dt, epsp, epsc, dmg, T, sig_xx, sig_yy, sig_zz, sig_xy, sig_yz, sig_zx,

           eps_xx, eps_yy, eps_zz, eps_xy, eps_yz, eps_zx, vx, vy, vz, x, y, z):



#   damage parameters

    global Wc, d1, d2, d3, d4, d5, eps_0, T_0, T_m

 

#   incremental plastic strain and strain rate

    depsp = epsp - epsp_old

    rate  = depsp / dt

 

#   principal stresses

    [s1, s2, s3] = eigval(sig_xx, sig_yy, sig_zz, sig_xy, sig_yz, sig_zx)

 

#   pressure and von Mises stress

    p      =-(s1+s2+s3)/3.0

    sig_vm = math.sqrt(1.5*( (s1+p)**2 + (s2+p)**2 + (s3+p)**2 ))

 

#   damage increment

    if (depsp > 0):

        dmg_cl = dmg_cl + max(0,s1,s2,s3)*depsp / Wc



        eps_f  = (d1 + d2*math.exp(d3*p/sig_vm)) * (1.0 + d4*math.log(rate/eps_0)) * (1.0 + d5*(T - T_0)/(T_m - T_0))

        dmg_jc = dmg_jc + depsp / eps_f 



    return [dmg_cl, dmg_jc, epsp] 

#

# COMPUTE PRINCIPAL STRESSES

def eigval(sig_xx, sig_yy, sig_zz, sig_xy, sig_yz, sig_zx):

 

#   constant, linear and quadratic terms in characteristic equation f = x^3 + a2*x^2 + a1*x + a0 = 0

    a0 =-sig_xx*sig_yy*sig_zz + sig_xx*sig_yz**2 + sig_xy**2*sig_zz + sig_zx**2*sig_yy - 2.0*sig_xy*sig_yz*sig_zx

    a1 =-sig_xy**2 - sig_yz**2 - sig_zx**2 + sig_yy*sig_zz + sig_xx*sig_yy + sig_xx*sig_zz

    a2 =-(sig_xx+sig_yy+sig_zz)



    Q  = a1/3.0 - a2**2/9.0

    Q  = min(0.0,Q)

    R  = a1*a2/6.0 - a0/2.0 - a2**3/27.0

    T  =-a2/3.0



    if (Q > -1.0e-10):

        cc    = 0.0

        ss    = 0.0

    else:

        S     = max(-1.0,min(1.0,R/math.sqrt(-Q**3)))

        theta = math.acos(S)

        Q2    = 2.0*math.sqrt(-Q)

        cc    = Q2*math.cos(theta/3.0)

        ss    = Q2*math.sin(theta/3.0)

 

#   principal stresses

    s1 = cc + T

    s2 =-cc/2.0 - math.sqrt(3.0)/2.0*ss + T

    s3 =-cc/2.0 + math.sqrt(3.0)/2.0*ss + T



    return [s1, s2, s3]

Results in ASCII file "damage_55.out":

#%center (10) 10
#%right (11) 11
#
#. Time
#$ Sensor ID
#! dmg_cl
#! dmg_jc
#! epsp
#
0.000000E+00 10 0.00000E+00 0.00000E+00 0.00000E+00
0.000000E+00 11 0.00000E+00 0.00000E+00 0.00000E+00
0.496146E-04 10 0.85364E-01 0.34469E+00 0.13540E+00
0.496146E-04 11 0.82269E-01 0.33053E+00 0.12927E+00
0.999605E-04 10 0.16470E+00 0.64550E+00 0.25662E+00
0.999605E-04 11 0.89230E-01 0.36157E+00 0.14233E+00
0.149887E-03 10 0.26081E+00 0.95341E+00 0.37574E+00
0.149887E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.199169E-03 10 0.28058E+00 0.10265E+01 0.40592E+00
0.199169E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.249532E-03 10 0.28062E+00 0.10268E+01 0.40604E+00
0.249532E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.299849E-03 10 0.28062E+00 0.10268E+01 0.40604E+00
0.299849E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.349016E-03 10 0.28062E+00 0.10268E+01 0.40604E+00
0.349016E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.399344E-03 10 0.28062E+00 0.10268E+01 0.40604E+00
0.399344E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.449704E-03 10 0.28070E+00 0.10272E+01 0.40620E+00
0.449704E-03 11 0.89561E-01 0.36351E+00 0.14321E+00
0.498831E-03 10 0.28070E+00 0.10272E+01 0.40620E+00
0.498831E-03 11 0.89561E-01 0.36351E+00 0.14321E+00