MAT_VISCO_PLASTIC
Material properties
"Optional title"
mid, $\rho$, $E$, $\nu$, did, tid
$\sigma_0$, $Q_1$, $C_1$, $Q_2$, $C_2$, cid, $c_{dec}$, $\alpha$
$\beta$, $m$, $T_0$, $T_m$, $n$
Parameter definition
Description
This is a non-linear visco-plastic constitutive model where the total stress $\boldsymbol{\sigma}$ is the sum of three terms:
$\boldsymbol{\sigma} = \boldsymbol{\sigma}^1 + \boldsymbol{\sigma}^2 + \boldsymbol{\sigma}^3$
$\boldsymbol{\sigma}^1$ is a non-linear viscous stress, $\boldsymbol{\sigma}^2$ is a non-linear elastic stress and $\boldsymbol{\sigma}^3$ is a linear elastic stress component. The rheological model is depicted below.
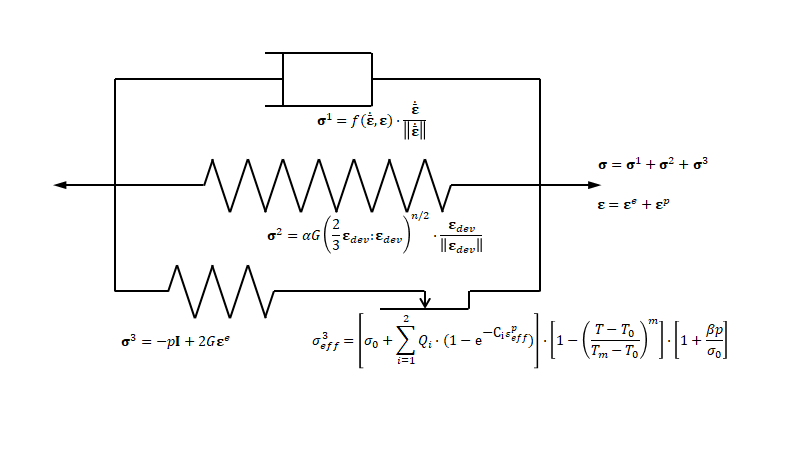
The non-linear viscous stress $\boldsymbol{\sigma}^1$ is defined as:
$\displaystyle{\boldsymbol{\sigma}^1 = f(\dot{\boldsymbol{\bar\varepsilon}}, \boldsymbol{\varepsilon}) \cdot \frac{\dot{\boldsymbol{\bar\varepsilon}}}{\vert\vert \dot{\boldsymbol{\bar\varepsilon}} \vert\vert}}$
where $f$ is a user defined FUNCTION or CURVE with ID cid. FUNCTION allows the viscosity to depend on both the effective geometric strain and the strain rate. If using a CURVE, the viscosity is a function of $\dot{\bar{\boldsymbol{\varepsilon}}}$ only. $\dot{\bar{\boldsymbol{\varepsilon}}}$ is a smeared out strain rate measure:
$\boldsymbol{\dot{\bar\varepsilon}}(t) = \displaystyle{\frac{1}{c_{dec}} \int_0^t} \dot{\boldsymbol{\varepsilon}}(\tau) \mathrm{e}^{-\tau/c_{dec}} \mathrm{d}\tau$
Note that $\dot{\bar{\boldsymbol{\varepsilon}}} = \dot{\boldsymbol{\varepsilon}}$ if $c_{dec}=0$. The non-linear elastic stress $\boldsymbol{\sigma}^2$ is defined to grow quadratically with the total deviatoric strain $\boldsymbol{\varepsilon}_{dev}$:
$\displaystyle{\boldsymbol{\sigma}^2 = 2 \alpha G \left( \displaystyle{\frac{2}{3}} \boldsymbol{\varepsilon}_{dev} : \boldsymbol{\varepsilon}_{dev} \right)^{n/2} \cdot \frac{\boldsymbol{\varepsilon}_{dev}}{\vert\vert \boldsymbol{\varepsilon}_{dev} \vert\vert} }$
$G$ is the linear shear modulus. The linear elastic stress component $\boldsymbol{\sigma}^3$ is defined as:
$\boldsymbol{\sigma}^3 = -p \mathbf{I} + 2 G \boldsymbol{\varepsilon}_{dev}^e$
$p$ is the hydrostatic pressure and $\boldsymbol{\varepsilon}_{dev}^e$ is the deviatoric part of the linear elastic strain tensor $\boldsymbol{\varepsilon}^e$ in the relation:
$\boldsymbol{\varepsilon} = \boldsymbol{\varepsilon}^e + \boldsymbol{\varepsilon}^p$
where $\boldsymbol{\varepsilon}^p$ is a plastic strain tensor. The plasticity model is based on a von Mises effective stress definition and an iso-choric plastic flow law. The plastic flow stress is defined as:
$\sigma_y = \left[ \sigma_0 + \displaystyle{\sum_{i=1}^2} Q_i (1 - \mathrm{e}^{-C_i \varepsilon_{eff}^p}) \right] \cdot \left[ 1 - \frac{T-T_0}{T_m-T_0}^m \right] \cdot \left[1 + \frac{\beta p}{\sigma_0} \right]$
Note that $\beta \neq 0$ leads to a pressure dependent plastic flow stress. $\beta \neq 0$ and an iso-choric plastic flow makes the flow rule non-associated. The hydrostatic pressure $p$ is defined as:
$p = -K \varepsilon_v + 3K \alpha_T (T-T_{ref})$
where $K$ is the linear bulk modulus, $\varepsilon_v$ is the volumetric strain. $\alpha_T$ is the thermal expansion coefficient and $T_{ref}$ is the reference temperature (see PROP_THERMAL).
Example
Gelatin like material
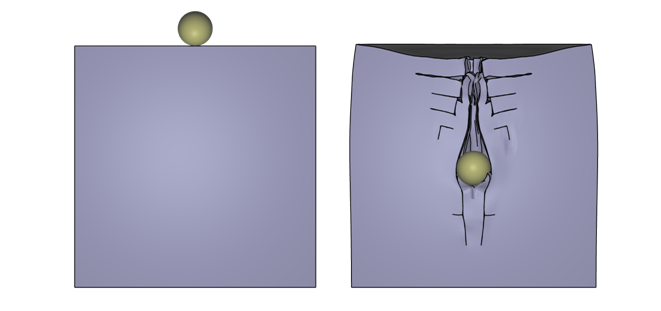
This is a complete model of a rigid sphere impacting a cylinder of a gelatin like visco-elastic material. Plasticity is turned off by setting the initial yield stress to a very large value. The FUNCTION with ID 20 defines the dynamic viscosity as a function of the total effective strain rate "rate" and the total geometrical strain "egeo".